(KR-KaggleKernelTranscription)Simple Exploration Notebook - Mercedes

Mercedes-Benz Greener Manufacturing 대회의 인기 커널 중 하나를 번역했습니다. 이번 포스트에선 높은 분류 성능을 자랑하기보다, EDA를 수행한 후 XGBoost와 Ramdom Forest모델을 활용하여 feature importance를 찾는 방법에 대해 알아봅니다.
- This notebook is written by SRK. Thanks for sharing!
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
import xgboost as xgb
color = sns.color_palette()
train_df = pd.read_csv("../Dataset/train.csv")
test_df = pd.read_csv("../Dataset/test.csv")
print("Train shape : ", train_df.shape)
print("Test shape : ", test_df.shape)
Train shape : (4209, 378)
Test shape : (4209, 377)
행의 수가 388개로 적습니다. 우리는 과적합에 유의할 필요가 있습니다. 상위 몇 개의 열들을 살펴 보도록 합시다.
train_df.head()
| ID | y | X0 | X1 | X2 | X3 | X4 | X5 | X6 | X8 | X10 | X11 | X12 | X13 | X14 | X15 | X16 | X17 | X18 | X19 | X20 | X21 | X22 | X23 | X24 | X26 | X27 | X28 | X29 | X30 | X31 | X32 | X33 | X34 | X35 | X36 | X37 | X38 | X39 | X40 | X41 | X42 | X43 | X44 | X45 | X46 | X47 | X48 | X49 | X50 | X51 | X52 | X53 | X54 | X55 | X56 | X57 | X58 | X59 | X60 | X61 | X62 | X63 | X64 | X65 | X66 | X67 | X68 | X69 | X70 | X71 | X73 | X74 | X75 | X76 | X77 | X78 | X79 | X80 | X81 | X82 | X83 | X84 | X85 | X86 | X87 | X88 | X89 | X90 | X91 | X92 | X93 | X94 | X95 | X96 | X97 | X98 | X99 | X100 | X101 | X102 | X103 | X104 | X105 | X106 | X107 | X108 | X109 | X110 | X111 | X112 | X113 | X114 | X115 | X116 | X117 | X118 | X119 | X120 | X122 | X123 | X124 | X125 | X126 | X127 | X128 | X129 | X130 | X131 | X132 | X133 | X134 | X135 | X136 | X137 | X138 | X139 | X140 | X141 | X142 | X143 | X144 | X145 | X146 | X147 | X148 | X150 | X151 | X152 | X153 | X154 | X155 | X156 | X157 | X158 | X159 | X160 | X161 | X162 | X163 | X164 | X165 | X166 | X167 | X168 | X169 | X170 | X171 | X172 | X173 | X174 | X175 | X176 | X177 | X178 | X179 | X180 | X181 | X182 | X183 | X184 | X185 | X186 | X187 | X189 | X190 | X191 | X192 | X194 | X195 | X196 | X197 | X198 | X199 | X200 | X201 | X202 | X203 | X204 | X205 | X206 | X207 | X208 | X209 | X210 | X211 | X212 | X213 | X214 | X215 | X216 | X217 | X218 | X219 | X220 | X221 | X222 | X223 | X224 | X225 | X226 | X227 | X228 | X229 | X230 | X231 | X232 | X233 | X234 | X235 | X236 | X237 | X238 | X239 | X240 | X241 | X242 | X243 | X244 | X245 | X246 | X247 | X248 | X249 | X250 | X251 | X252 | X253 | X254 | X255 | X256 | X257 | X258 | X259 | X260 | X261 | X262 | X263 | X264 | X265 | X266 | X267 | X268 | X269 | X270 | X271 | X272 | X273 | X274 | X275 | X276 | X277 | X278 | X279 | X280 | X281 | X282 | X283 | X284 | X285 | X286 | X287 | X288 | X289 | X290 | X291 | X292 | X293 | X294 | X295 | X296 | X297 | X298 | X299 | X300 | X301 | X302 | X304 | X305 | X306 | X307 | X308 | X309 | X310 | X311 | X312 | X313 | X314 | X315 | X316 | X317 | X318 | X319 | X320 | X321 | X322 | X323 | X324 | X325 | X326 | X327 | X328 | X329 | X330 | X331 | X332 | X333 | X334 | X335 | X336 | X337 | X338 | X339 | X340 | X341 | X342 | X343 | X344 | X345 | X346 | X347 | X348 | X349 | X350 | X351 | X352 | X353 | X354 | X355 | X356 | X357 | X358 | X359 | X360 | X361 | X362 | X363 | X364 | X365 | X366 | X367 | X368 | X369 | X370 | X371 | X372 | X373 | X374 | X375 | X376 | X377 | X378 | X379 | X380 | X382 | X383 | X384 | X385 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 130.81 | k | v | at | a | d | u | j | o | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 6 | 88.53 | k | t | av | e | d | y | l | o | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 7 | 76.26 | az | w | n | c | d | x | j | x | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 9 | 80.62 | az | t | n | f | d | x | l | e | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 13 | 78.02 | az | v | n | f | d | h | d | n | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Target Variable:
“y”는 우리가 예측해야 하는 변수입니다. 먼저 이 변수에 대한 분석을 수행해 봅시다.
plt.figure(figsize=(8,6))
plt.scatter(range(train_df.shape[0]), np.sort(train_df.y.values))
plt.xlabel('index', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.show()
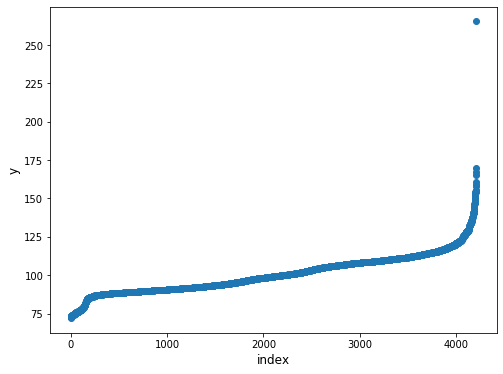
하나의 데이터 포인트가 다른 데이터들보다 훨씬 위에 있는 것처럼 보입니다.
이제 분포 그래프(distribution graph)를 그려 봅시다.
ulimit = 180
train_df['y'].ix[train_df['y']>ulimit] = ulimit
plt.figure(figsize=(12,8))
sns.distplot(train_df.y.values, bins=50, kde=False)
plt.xlabel('y value', fontsize=12)
plt.show()
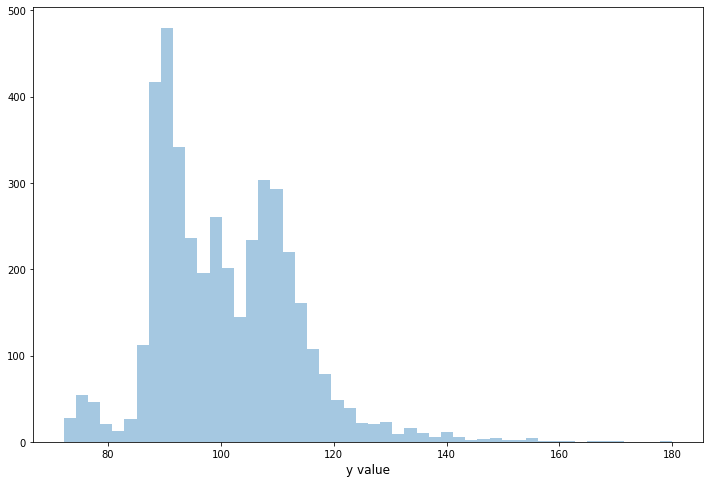
이제 데이터셋에 있는 모든 변수의 데이터 타입을 살펴보겠습니다.
dtype_df = train_df.dtypes.reset_index()
dtype_df.columns = ["Count", "Column Type"]
dtype_df.groupby("Column Type").aggregate('count').reset_index()
| Column Type | Count | |
|---|---|---|
| 0 | int64 | 369 |
| 1 | float64 | 1 |
| 2 | object | 8 |
대부분의 열은 8개의 범주형(categorical) 열과 1개의 float타입 열(target variable)을 갖고 있습니다.
dtype_df.ix[:10,:]
| Count | Column Type | |
|---|---|---|
| 0 | ID | int64 |
| 1 | y | float64 |
| 2 | X0 | object |
| 3 | X1 | object |
| 4 | X2 | object |
| 5 | X3 | object |
| 6 | X4 | object |
| 7 | X5 | object |
| 8 | X6 | object |
| 9 | X8 | object |
| 10 | X10 | int64 |
X0부터 X8까지는 범주형 열들입니다.
Missing values:
이제 누락된 값들을 확인해 보겠습니다.
missing_df = train_df.isnull().sum(axis=0).reset_index()
missing_df.columns = ['column_name', 'missing_count']
missing_df = missing_df.ix[missing_df['missing_count']>0]
missing_df = missing_df.sort_values(by='missing_count')
missing_df
| column_name | missing_count |
|---|
데이터셋에 누락된값이 없는 것으로 확인됩니다.
정수형 열(Integer columns) 분석해보기:
unique_values_dict = {}
for col in train_df.columns:
if col not in ["ID", "y", "X0", "X1", "X2", "X3", "X4", "X5", "X6", "X8"]:
unique_value = str(np.sort(train_df[col].unique()).tolist())
tlist = unique_values_dict.get(unique_value, [])
tlist.append(col)
unique_values_dict[unique_value] = tlist[:]
for unique_val, columns in unique_values_dict.items():
print("Columns containing the unique values : ",unique_val)
print(columns)
print("--------------------------------------------------")
Columns containing the unique values : [0, 1]
['X10', 'X12', 'X13', 'X14', 'X15', 'X16', 'X17', 'X18', 'X19', 'X20', 'X21', 'X22', 'X23', 'X24', 'X26', 'X27', 'X28', 'X29', 'X30', 'X31', 'X32', 'X33', 'X34', 'X35', 'X36', 'X37', 'X38', 'X39', 'X40', 'X41', 'X42', 'X43', 'X44', 'X45', 'X46', 'X47', 'X48', 'X49', 'X50', 'X51', 'X52', 'X53', 'X54', 'X55', 'X56', 'X57', 'X58', 'X59', 'X60', 'X61', 'X62', 'X63', 'X64', 'X65', 'X66', 'X67', 'X68', 'X69', 'X70', 'X71', 'X73', 'X74', 'X75', 'X76', 'X77', 'X78', 'X79', 'X80', 'X81', 'X82', 'X83', 'X84', 'X85', 'X86', 'X87', 'X88', 'X89', 'X90', 'X91', 'X92', 'X94', 'X95', 'X96', 'X97', 'X98', 'X99', 'X100', 'X101', 'X102', 'X103', 'X104', 'X105', 'X106', 'X108', 'X109', 'X110', 'X111', 'X112', 'X113', 'X114', 'X115', 'X116', 'X117', 'X118', 'X119', 'X120', 'X122', 'X123', 'X124', 'X125', 'X126', 'X127', 'X128', 'X129', 'X130', 'X131', 'X132', 'X133', 'X134', 'X135', 'X136', 'X137', 'X138', 'X139', 'X140', 'X141', 'X142', 'X143', 'X144', 'X145', 'X146', 'X147', 'X148', 'X150', 'X151', 'X152', 'X153', 'X154', 'X155', 'X156', 'X157', 'X158', 'X159', 'X160', 'X161', 'X162', 'X163', 'X164', 'X165', 'X166', 'X167', 'X168', 'X169', 'X170', 'X171', 'X172', 'X173', 'X174', 'X175', 'X176', 'X177', 'X178', 'X179', 'X180', 'X181', 'X182', 'X183', 'X184', 'X185', 'X186', 'X187', 'X189', 'X190', 'X191', 'X192', 'X194', 'X195', 'X196', 'X197', 'X198', 'X199', 'X200', 'X201', 'X202', 'X203', 'X204', 'X205', 'X206', 'X207', 'X208', 'X209', 'X210', 'X211', 'X212', 'X213', 'X214', 'X215', 'X216', 'X217', 'X218', 'X219', 'X220', 'X221', 'X222', 'X223', 'X224', 'X225', 'X226', 'X227', 'X228', 'X229', 'X230', 'X231', 'X232', 'X234', 'X236', 'X237', 'X238', 'X239', 'X240', 'X241', 'X242', 'X243', 'X244', 'X245', 'X246', 'X247', 'X248', 'X249', 'X250', 'X251', 'X252', 'X253', 'X254', 'X255', 'X256', 'X257', 'X258', 'X259', 'X260', 'X261', 'X262', 'X263', 'X264', 'X265', 'X266', 'X267', 'X269', 'X270', 'X271', 'X272', 'X273', 'X274', 'X275', 'X276', 'X277', 'X278', 'X279', 'X280', 'X281', 'X282', 'X283', 'X284', 'X285', 'X286', 'X287', 'X288', 'X291', 'X292', 'X294', 'X295', 'X296', 'X298', 'X299', 'X300', 'X301', 'X302', 'X304', 'X305', 'X306', 'X307', 'X308', 'X309', 'X310', 'X311', 'X312', 'X313', 'X314', 'X315', 'X316', 'X317', 'X318', 'X319', 'X320', 'X321', 'X322', 'X323', 'X324', 'X325', 'X326', 'X327', 'X328', 'X329', 'X331', 'X332', 'X333', 'X334', 'X335', 'X336', 'X337', 'X338', 'X339', 'X340', 'X341', 'X342', 'X343', 'X344', 'X345', 'X346', 'X348', 'X349', 'X350', 'X351', 'X352', 'X353', 'X354', 'X355', 'X356', 'X357', 'X358', 'X359', 'X360', 'X361', 'X362', 'X363', 'X364', 'X365', 'X366', 'X367', 'X368', 'X369', 'X370', 'X371', 'X372', 'X373', 'X374', 'X375', 'X376', 'X377', 'X378', 'X379', 'X380', 'X382', 'X383', 'X384', 'X385']
--------------------------------------------------
Columns containing the unique values : [0]
['X11', 'X93', 'X107', 'X233', 'X235', 'X268', 'X289', 'X290', 'X293', 'X297', 'X330', 'X347']
--------------------------------------------------
모든 정수 열들은 2진수이며, 일부 열은 고유한 값인 0을 갖고 있습니다. 우리는 이러한 열들에 대해 모델링 과정에서 제외할 수 있습니다.
이제 데이터셋에 있는 범주형 열들에 대해 탐색해 보겠습니다.
var_name = "X0"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.stripplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
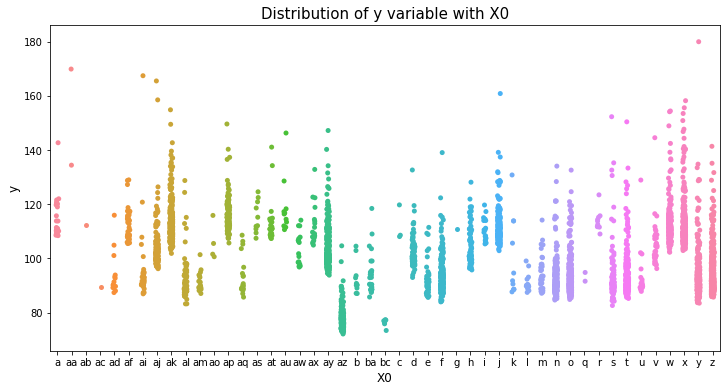
var_name = "X1"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.stripplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
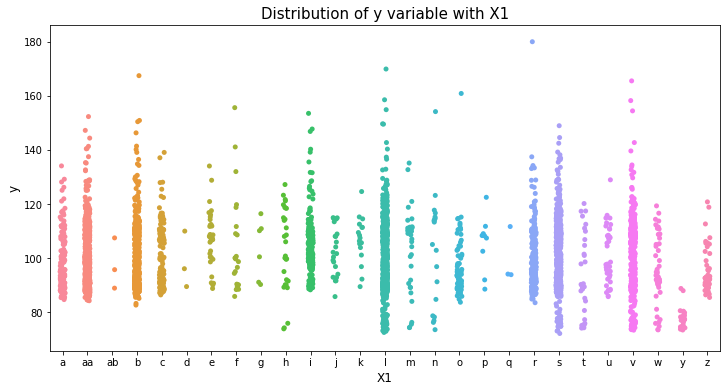
var_name = "X2"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.boxplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
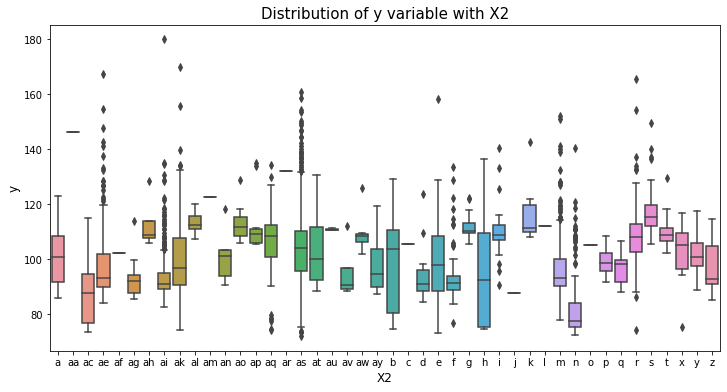
var_name = "X3"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.violinplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
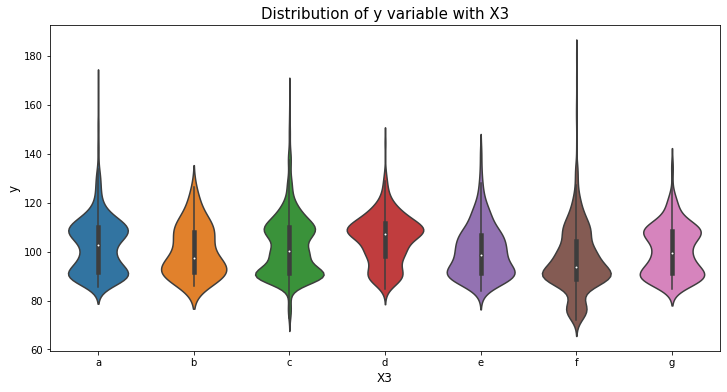
var_name = "X4"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.violinplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
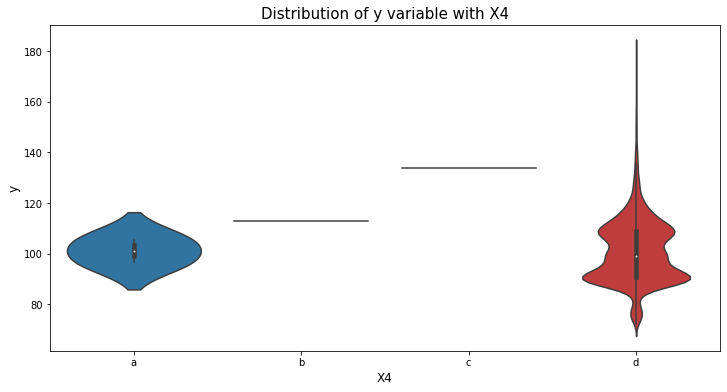
var_name = "X5"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.boxplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
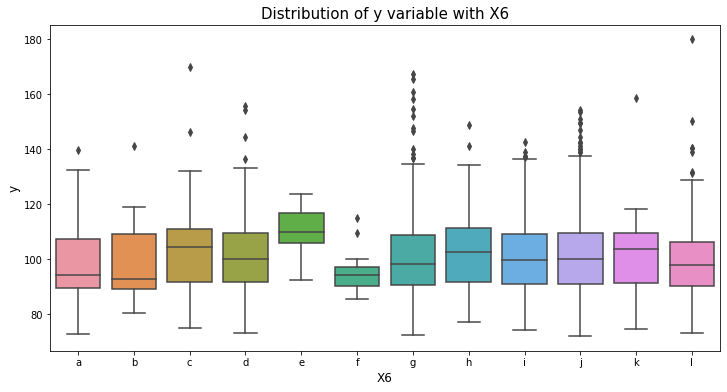
var_name = "X6"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.boxplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
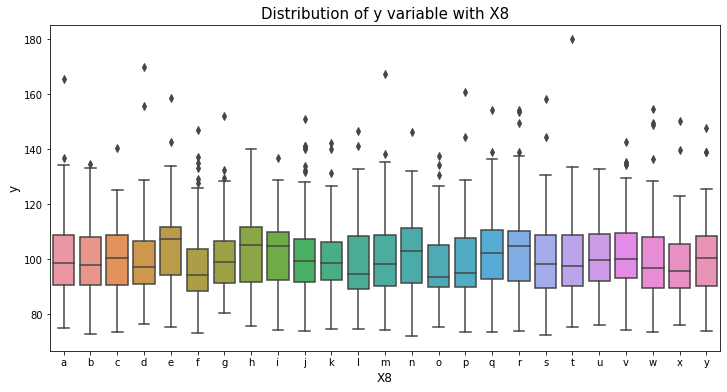
var_name = "X8"
col_order = np.sort(train_df[var_name].unique()).tolist()
plt.figure(figsize=(12,6))
sns.boxplot(x=var_name, y='y', data=train_df, order=col_order)
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
이진 변수들에 대해 탐색해보기:
이제 우리는 이진 변수들에 대해 탐색해볼 것입니다. 우리가 이전에 보았던 것들 중 상당수가 있는 것을 볼 수 있습니다. 이 변수들 중에서 0과 1의 값을 얻어오는 것으로 시작해 봅시다.
zero_count_list = []
one_count_list = []
cols_list = unique_values_dict['[0, 1]']
for col in cols_list:
zero_count_list.append((train_df[col]==0).sum())
one_count_list.append((train_df[col]==1).sum())
N = len(cols_list)
ind = np.arange(N)
width = 0.35
plt.figure(figsize=(6,100))
p1 = plt.barh(ind, zero_count_list, width, color='red')
p2 = plt.barh(ind, one_count_list, width, left=zero_count_list, color="blue")
plt.yticks(ind, cols_list)
plt.legend((p1[0], p2[0]), ('Zero count', 'One Count'))
plt.show()

이제 각각의 이진 변수에서 평균 y값을 확인해 보겠습니다.
zero_mean_list = []
one_mean_list = []
cols_list = unique_values_dict['[0, 1]']
for col in cols_list:
zero_mean_list.append(train_df.ix[train_df[col]==0].y.mean())
one_mean_list.append(train_df.ix[train_df[col]==1].y.mean())
new_df = pd.DataFrame({"column_name":cols_list+cols_list, "value":[0]*len(cols_list) + [1]*len(cols_list), "y_mean":zero_mean_list+one_mean_list})
new_df = new_df.pivot('column_name', 'value', 'y_mean')
plt.figure(figsize=(8,80))
sns.heatmap(new_df)
plt.title("Mean of y value across binary variables", fontsize=15)
plt.show()

위의 그래프에서 0~1 사이의 고른 색상 차이를 보여주는 이진 변수는 더 좋은 예측 결과를 보여줄 수 있는데, 두 클래스 간의 카운트 분포(count distribution)가 양호한 경우도 마찬가지로 더 좋은 예측 결과를 보여줄 수 있습니다. (이전 그래프에서 볼 수 있음). 우리는 이 노트북의 뒷부분에서 중요한 변수들에 대해 더 자세히 살펴볼 것입니다.
ID variable:
우리가 살펴 봐야 할 중요한 것은 ID 변수(ID variable)입니다. 이 변수는 train과 test 과정을 위해 어떻게 데이터셋을 쪼갤지에 대한 아이디어를 제공해 줍니다.(랜덤 또는 id 기반 등) 그리고 ID가 예측 성능에 대해 잠재적으로 도움을 줄 수 있는지 확인하는데 도움이 됩니다. (아마 비즈니스에는 도움이 되지 않을 수 있습니다.)
먼저 ‘y’ 변수가 ID 변수를 통해 어떻게 변경되는지 살펴 보겠습니다.
var_name = "ID"
plt.figure(figsize=(12,6))
sns.regplot(x=var_name, y='y', data=train_df, scatter_kws={'alpha':0.5, 's':30})
plt.xlabel(var_name, fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of y variable with "+var_name, fontsize=15)
plt.show()
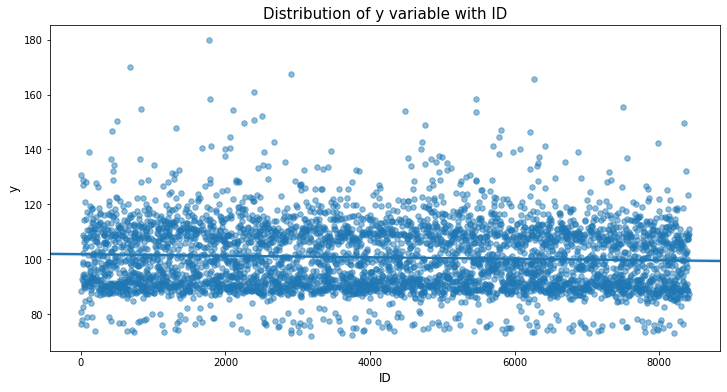
ID 변수와 관련하여 약간 감소하는 경향이 있는 것으로 보입니다. 이제 train과 test 간에 ID 변수가 어떻게 분포하고 있는지 살펴 보겠습니다.
plt.figure(figsize=(6,10))
train_df['eval_set'] = "train"
test_df['eval_set'] = "test"
full_df = pd.concat([train_df[["ID","eval_set"]], test_df[["ID","eval_set"]]], axis=0)
plt.figure(figsize=(12,6))
sns.violinplot(x="eval_set", y='ID', data=full_df)
plt.xlabel("eval_set", fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title("Distribution of ID variable with evaluation set", fontsize=15)
plt.show()
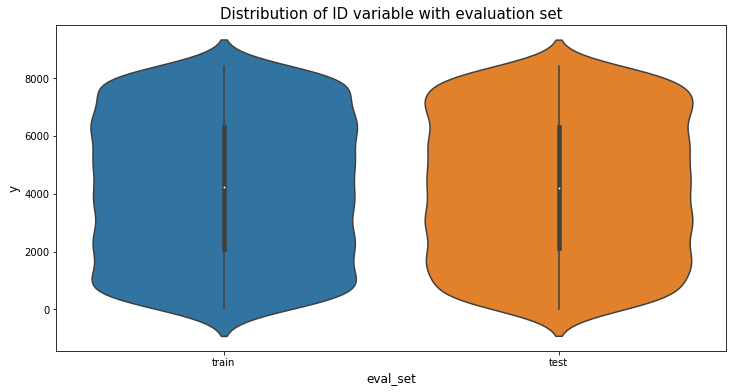
train과 test 샘플 사이에 random split을 통해 임의로 분할한 것 같습니다.
중요 변수들:
이제 XGBoost 모델을 사용하여 중요한 변수들을 얻어 보도록 하겠습니다.
for f in ["X0", "X1", "X2", "X3", "X4", "X5", "X6", "X8"]:
lbl = preprocessing.LabelEncoder()
lbl.fit(list(train_df[f].values))
train_df[f] = lbl.transform(list(train_df[f].values))
train_y = train_df['y'].values
train_X = train_df.drop(["ID", "y", "eval_set"], axis=1)
# Thanks to anokas for this #
def xgb_r2_score(preds, dtrain):
labels = dtrain.get_label()
return 'r2', r2_score(labels, preds)
xgb_params = {
'eta': 0.05,
'max_depth': 6,
'subsample': 0.7,
'colsample_bytree': 0.7,
'objective': 'reg:linear',
'silent': 1
}
dtrain = xgb.DMatrix(train_X, train_y, feature_names=train_X.columns.values)
model = xgb.train(dict(xgb_params, silent=0), dtrain, num_boost_round=100, feval=xgb_r2_score, maximize=True)
# plot the important features #
fig, ax = plt.subplots(figsize=(12,18))
xgb.plot_importance(model, max_num_features=50, height=0.8, ax=ax)
plt.show()
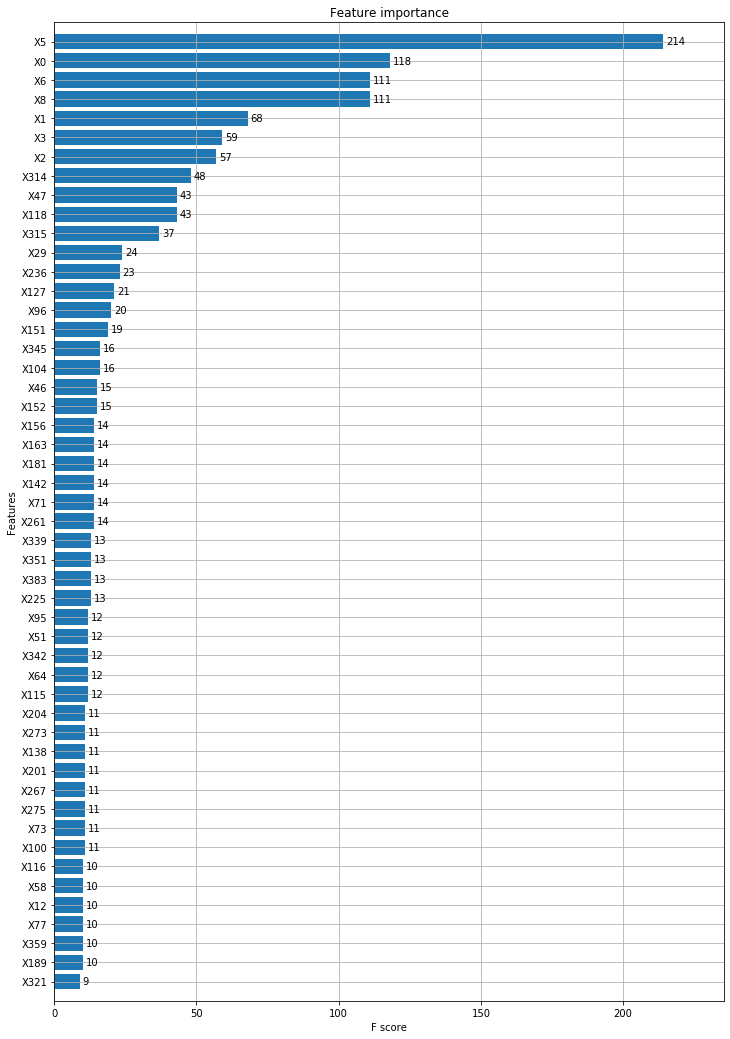
범주형 변수들이 이진 변수들에 비해 높은 자리를 차지하고 있습니다.
랜덤 포레스트 모델을 만들고 중요한 변수들을 확인해 봅시다
from sklearn import ensemble
model = ensemble.RandomForestRegressor(n_estimators=200, max_depth=10, min_samples_leaf=4, max_features=0.2, n_jobs=-1, random_state=0)
model.fit(train_X, train_y)
feat_names = train_X.columns.values
## plot the importances ##
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1][:20]
plt.figure(figsize=(12,12))
plt.title("Feature importances")
plt.bar(range(len(indices)), importances[indices], color="r", align="center")
plt.xticks(range(len(indices)), feat_names[indices], rotation='vertical')
plt.xlim([-1, len(indices)])
plt.show()
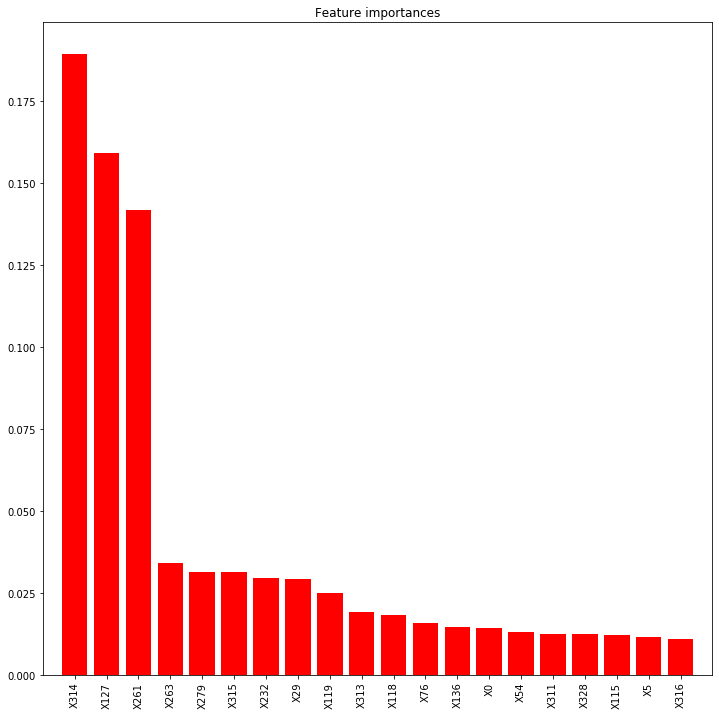
XGBoost와 랜덤 포레스트 간 중요 변수들에 차이가 꽤 있습니다. 왜 그런지는 잘 모르겠습니다.
곧 업데이트하겠습니다.!
