(Normalization) BN이후의 다양한 정규화 기법들

27 Sep 2019 in Devlog / MLDLStudy on Nn methodology, Dl, Normalization

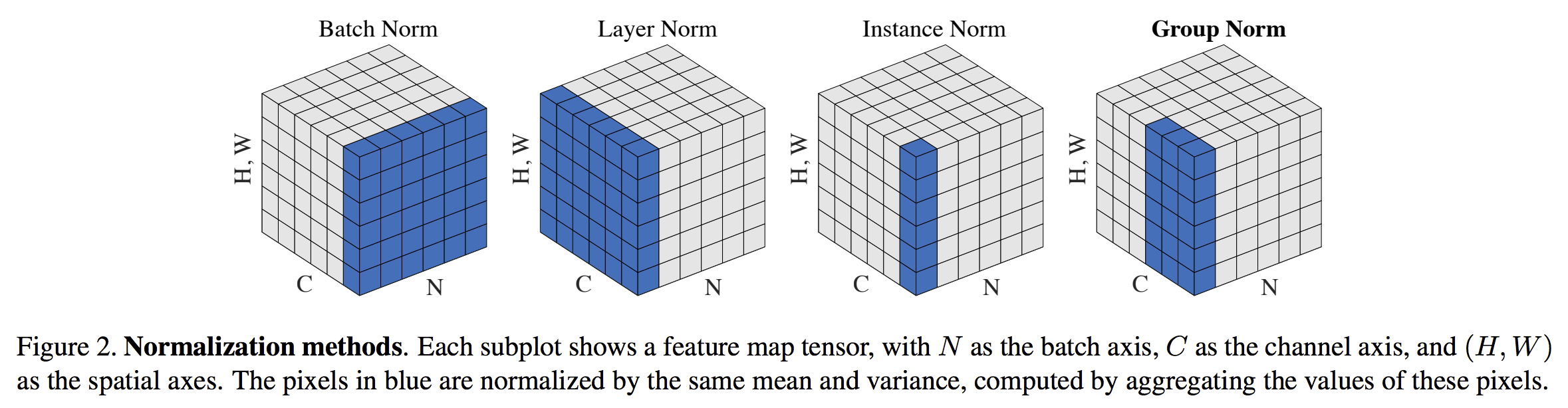
Batch Normalization 이후의 다양한 정규화 기법들에 대해 알아봅니다.

본 글은 개인적으로 스터디하며 정리한 자료입니다. 간혹 레퍼런스를 찾지 못해 빈 곳이 있으므로 양해 부탁드립니다.

Weight Normalization(WN)

• Weight normalization은 mini-batch를 정규화하는 것이 아니라 layer의 가중치를 정규화
• Weight normalization은 레이어의 가중치 w를 다음과 같이 재매개변수화(reparametrization)한다.
  $w=\frac{g}{|v|}v$
• BN과 비슷하게 WN은 표현(expressiveness)을 줄이지 않고 가중치 벡터의 크기와 방향을 분리한다. (BN에서 입력값을 표준편차로 나누어 주는 것과 비슷한 효과)
• 이후 Gradient descent기법(경사하강법)으로 g, v를 최적화하며, 이는 학습의 최적화를 쉽게 만듬. WN은 경우에 따라 BN보다 빠름.
• CNN의 경우 가중치의 수는 입력의 수보다 훨씬 작으며, 이는 즉 BN보다 WN이 연산량이 훨씬 적음을 의미. (BN의 경우 입력값의 모든 원소를 연산해야 하고, 이미지 등의 고차원 데이터에서 연산이 매우 많아진다.)
• WN은 그 자체만으로도 모델 훈련에 도움을 주지만 mean-only batch normalization(입력을 표준편차로 나누거나 scale 재조정을 하지 않는 BN)과 함께 사용하는 것을 권장
  • 표준편차를 계산하지 않기 때문에 BN보다 연산량이 적음.
  • 활성값의 평균을 v와 독립시킬 수 있다. (WN은 활성화값의 평균과 레이어의 가중치를 독립적으로 분리할 수 없으므로 각 레이어의 평균간에 높은 종속성이 발생. mean-only batch normalization를 사용하면 이런 문제를 해결할 수 있다고 주장)
  • 활성화에 gentler noise를 추가 (BN의 부작용 중 하나는 mini-batch에서 계산된 노이즈가 많은 추정값을 사용해 활성화값에 확률적인 잡음을 추가한다는 것이며, 일부 문제에서 이런 노이즈는 규제의 역할을 수행하지만 강화 학습과 같이 노이즈에 예민한 태스크에서는 성능을 낮춘다.)
    • 이 경우 mean-only batch normalization과 WN을 함께 사용하면 큰 수의 법칙에 따라 노이즈가 정규 분포의 형태를 띄며, 이는 노이즈가 완만하다고 할 수 있다.
    • BN과 비교해 훈련 과정에서 노이즈가 줄어들게 된다.
    • CIFAR-10모델에서 이미지 분류 문제를 해결할 때 WN이 특히 잘 작동한다고 함.

Layer Normalization(LN)

BN과 유사한 형태를 지니며, mini-batch의 feature 수가 같아야 한다.

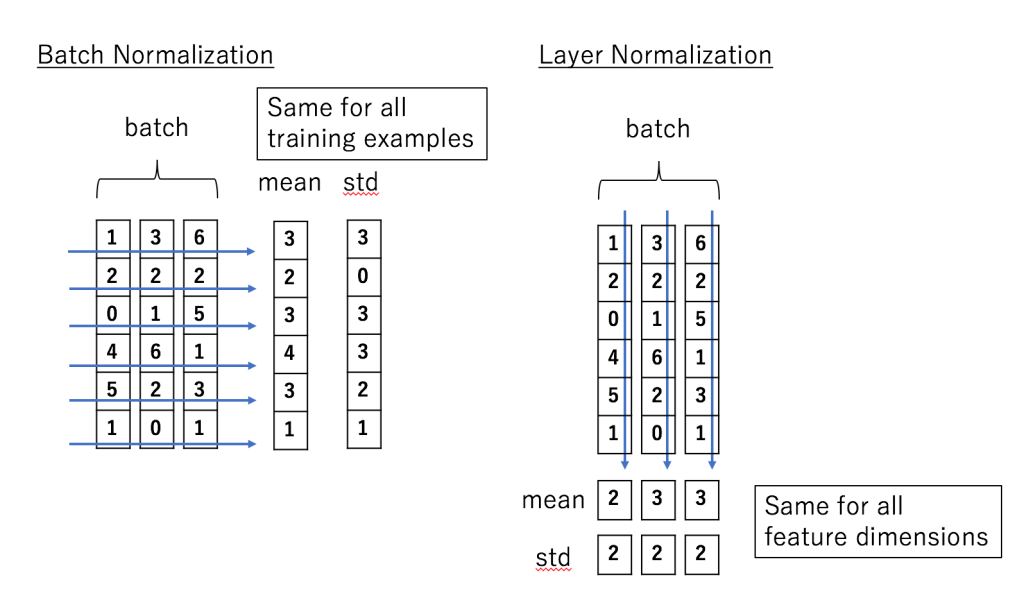
• BN과 LN의 차이점
  • BN은 batch 차원에서의 정규화, LN은 feature 차원에서의 정규화임에 유의
  • BN은 batch 전체에서 계산이 이루어지며, 각 batch에서 동일하게 계산함.
  • LN은 각 특성(feature)에 대해 따로 계산이 이루어지며 각 특성에 독립적으로 계산함. (hidden unit)
  • LN은 batch size와 상관이 없으므로 RNN에서 매우 좋은 성능을 보인다.

Instance Normalization(IN)

• LN과 유사하지만 한단계 더 나아가 평균과 표준편차를 구해 각 example의 채널에 대해 정규화를 진행.
• Style transfer를 위해 고안되었으며, 네트워크가 원본 이미지와 변형된 이미지를 구분할 수 없기를 바라며 설계되었음. </b>이미지에 국한된 정규화</b>이므로 따라서 RNN에는 사용할 수 없다.
• Style transfer, GAN 등의 태스크에서 BN을 대체해 주로 사용하고, real-time generation에 효과적인 방식이다.

Group Normalization(GN)

• Instance Normalization(IN)과 유사하지만 채널을 그룹으로 묶어 평균과 표준편차를 구한다는 것에 차이가 존재한다.
• Group normalization은 IN과 LN의 중간이라고 볼 수 있다.
  • 모든 채널이 단일 그룹에 있으면 LN
  • 각 채널을 다른 그룹에 배치하면 IN
• Group normalization은 ImageNet에서 배치 사이즈가 32일 때 BN과 거의 근접한 성능을 보였다.
  • 32보다 더 작은 사이즈에 대해서는 더 좋은 성능을 보임.
  • Object detection 또는 더 높은 해상도의 이미지를 사용하는 작업(메모리의 제약이 있는 작업)에서 매우 효과적임.
• 왜 GN이 LN, IN보다 효과적인가?
  • LN은 모든 채널이 동등하게 중요하다라는 가정 하에 정규화(평균 계산)가 진행됨
  • Image의 경우 하지만 가장자리와 중심부의 중요성이 다르며, 즉 여러 채널에서 서로 다르게 계산하면 모델에 따라 유연성을 제공해 줄 수 있음.
  • 이미지의 경우 각 채널은 독립된 것이 아니므로(IN) 주변 채널을 활용해 더 정규화를 넓게 적용할 수 있다.

Batch Renormalization

• BN을 small batch size로 사용하기 위한 방법으로, 추론 시 BN의 개별 mini-batch 통계값들을 사용하지 않음.
• Mini-batch에서 이동평균을 사용하며, 이는 개별 mini-batch보다 실제 평균과 분산값을 더 잘 예측하기 위한 방법.
• 훈련에는 왜 이동평균을 사용하지 않는가?
  • 데이터 정규화에 있어 통계를 사용하려면 이 값을 역전파시키는 방법에 대해 적절한 방안이 있어야 함.
  • 이전 mini-batch의 활성화 통계값을 사용해 정규화를 진행하는 경우 역전파 중 이전 레이어가 통계값에 얼마나 영향을 미쳤는지 계산해야 한다. (이러한 상호 작용을 무시하면 이전 레이어의 loss에 아무 영향을 미치지 않더라도 활성화값이 계속 증가할 수 있음.)
• 훈련 과정에서 이동 평균을 사용하면 모든 이전 mini-batch값의 통계값을 저장해야 하므로 연산량이 매우 많아짐.
  • 논문 저자는 이동평균을 사용하면서 통계에 대한 이전 계층의 영향을 고려하도록 제안
  • 이동평균을 이용해 재매개변수화하는 것이 이 방법의 핵심
• 이동 평균의 평균값을 $\mu$, 편차를 $\sigma$, mini-batch의 평균과 편차를 $\mu_{B}$, $\sigma_{B}$ 라고 한다면 Batch renormalization은 다음과 같이 표현할 수 있다.
  • $\frac{x_i-\mu}{\sigma}=\frac{x_i-\mu_B}{\sigma_B}\times r+d$, $where\ r=\frac{\sigma_B}{\sigma},\ d=\frac{\mu_B-\mu}{\sigma}$
  • 즉 이동 평균 통계값과 mini-batch에서 얻은 통계값으로 BN에 곱하고 더해 정규화 수행.
• BN의 초기화 설정, 빠른 속도 등의 이점을 가지며 BN과 마찬가지로 batch renormalization의 성능 또한 배치 크기가 감소할 때 여전히 저하되는 문제가 존재.

Batch-Instance normalization(BIN)

• Batch-Instance Normalization for Adaptively Style-Invariant Neural Networks : 이미지에서 style과 contrast의 차이를 설명하기 위해 IN을 확장한 정규화 기법. (저자 블로그 참고링크)
  • 입력 영상이 style vatiation은 영상 인식에 유의미한 정보를 전달하지만 때로 불필요한 복잡도를 야기해 모델 학습에 방해가 된다.
  • BIN은 이미지에서 중요한 style 정보는 유지하고 불필요한 style vatiation은 제거함으로서 모델 학습을 용이하게 하는 normalization기법.
• IN(Instance Normalization)의 문제점은 style정보를 완전히 지운다는 것에 있음.
  • Style transfer에는 유용할 수 있으나 weather classification과 같이 스타일이 중요한 특징이 될 때는 문제가 될 수 있다.
  • 제거해야 하는 style 정보의 정도는 작업에 따라 다르지만 BIN은 각 작업과 특성 맵(채널)에 대해 style 정보의 양을 파악해 처리하려고 함.
• BN의 output과 IN의 output을 각각 ${\hat{x}}^{(B)}$, ${\hat{x}}^{(I)}$ 라고 하면 BIN output($y$)는 다음과 같은 수식으로 표현할 수 있다.
  $y=(\rho\times{\hat{x}}^{(B)}+(1-\rho)\times{\hat{x}}^{(I)})\times\gamma+\beta$
• BIN은 BN과 IN의 보간과 같으며, balance변수 $\rho$는 경사하강법을 통해 학습할 수 있는 trainable variable이다.
• BIN은 CIFAR-10/100, ImageNet, domain adaption, style transfer 부문에서 BN을 능가했음.
  • 이미지 분류에서 $\rho$값은 0 또는 1에 가까워지는데, 이는 많은 layer가 instance normalization 또는 BN만 사용했음을 알 수 있게 해준다.
  • Layer들은 IN보다 BN을 사용하는 경향이 있는데, 이는 IN이 불필요한 style transfer를 제거하는 방법으로 더 많이 작용하기 때문.
  • 반면 style transfer에서는 반대의 경향이 나타나며, 이는 주어진 style이 style transfer에서 덜 중요하다는 사실을 나타냄.
• BIN에서 $\rho$에 높은 learning rate를 적용하면 성능이 향상된다고 주장.
• BIN은 정규화 방법이 경사하강법으로 다른 정규화 방법을 배울 수 있지 않을까? 라는 의문을 제기.

Switchable Normalization

• BN, IN, LN 등의 다양한 정규화 기법의 사용에 있어서 전환 가능한 정규화 방법을 제안.
• 전환에 대한 가중치는 경사하강법을 통해 학습.
• 이미지 분류, object detection 등에 있어서 BN보다 우수함을 보임.

Spectral Normalization

• GAN 훈련을 향상시키기 위해 판별자의 Lipschitz 상수를 제한
• 최소한의 조정으로 GAN의 학습을 개선했음.